・Lobe dynamicsにもとづく軌道設計,制御(2022年4月ー現在)
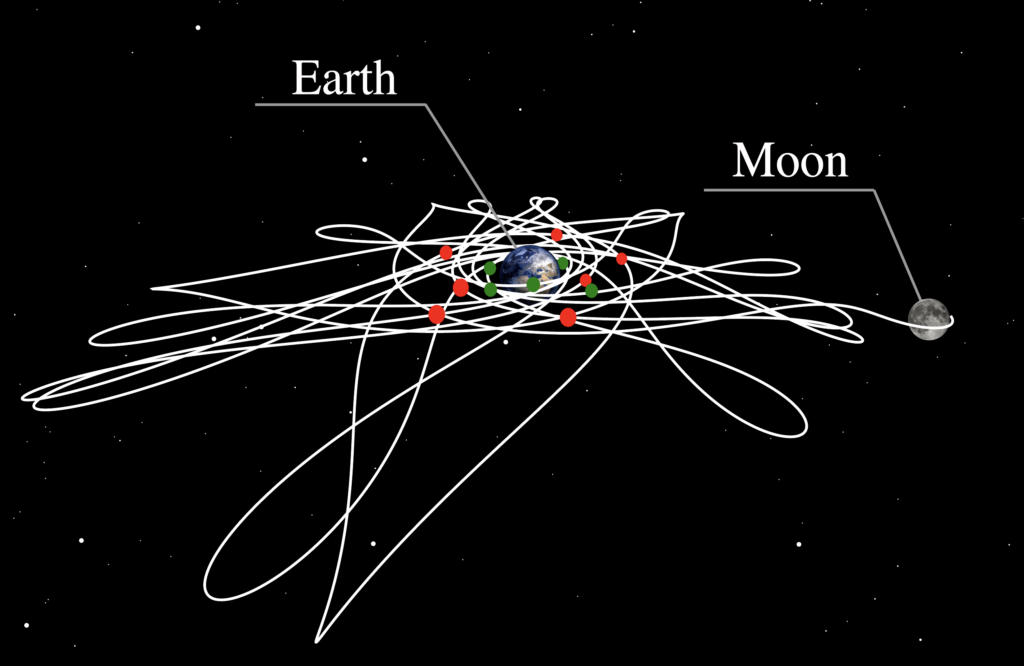
宇宙探査機のダイナミクスは,複数天体の重力の影響を受け,カオス的で非線形性が強いことが知られている.この特徴により,目的地に到達するための最適な軌道を数値的に探索することは難しい.そこで,燃料消費を少なくするために,力学的構造の1つである不変多様体に着目することが重要である.
不変多様体を利用したものの1つがlobe dynamicsである.Lobe dynamicsは,たとえば共鳴軌道の安定・不安定多様体によって囲まれた「lobe」という領域に注目することで,カオス的な軌道の遷移構造を捉えることができる.このような複雑な構造のためこれまでlobe dynamicsはあまり利用されてこなかったが,この遷移構造を利用することで軌道設計段階でカオス的な挙動を取り入れることができ,より燃料を必要としない軌道を見つけることができる.
この研究では,lobe dynamicsにもとづいてカオス的遷移軌道を解析し,新しい軌道設計・制御手法を提案する.近点ポアンカレマップ上で共鳴軌道の安定・不安定多様体に囲まれたlobeを網羅的に特定し,どのlobeからどのlobeに遷移するのかを明らかにする.このlobeの遷移順序を理解することにより,適切な入力を加えることで複数のlobeの遷移を組み合わせて大きな軌道遷移を実現する.
研究成果の一部はこちらの論文(Phys. Rev. Res.)から.
・凸最適化による低推力軌道の最適化(2021年8月ー現在)
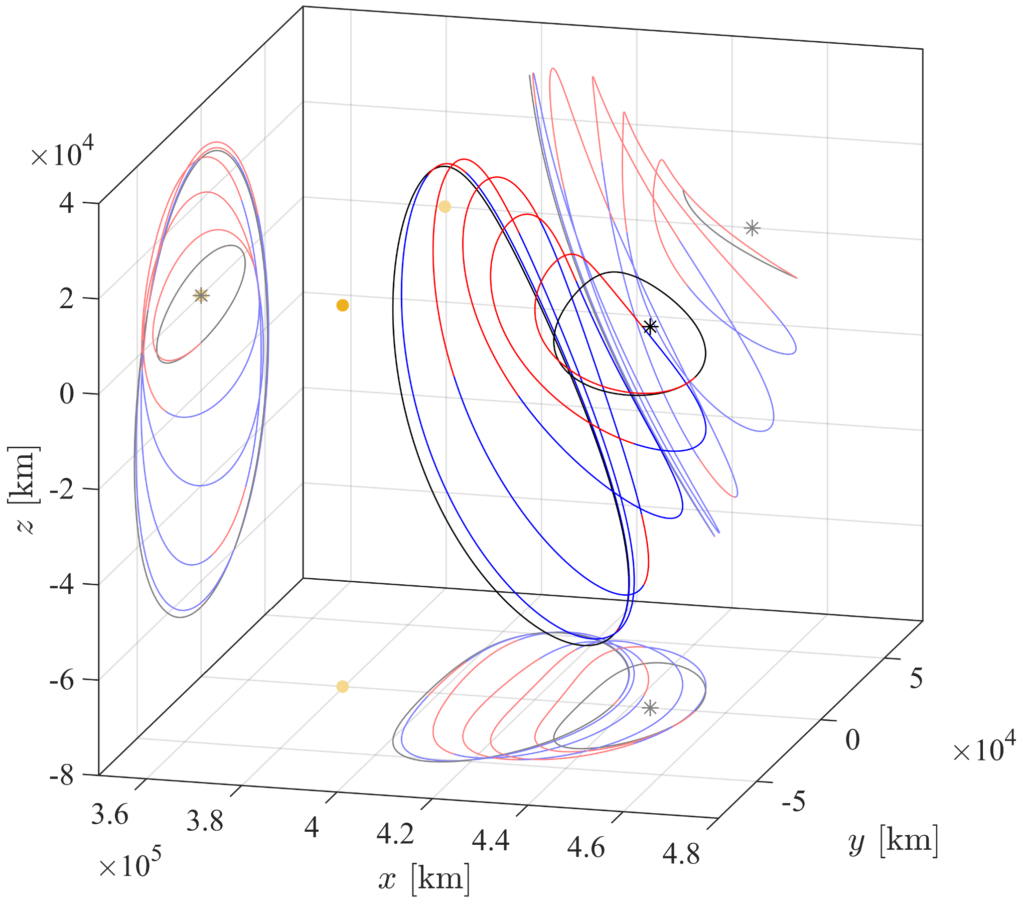
イオンエンジンやソーラーセイルのような低推力推進は,比推力が高く高効率であるため近年よく用いられている.低推力推進により効率よく深宇宙探査を行うことができるが,不安定な力学的環境では初期値鋭敏性により最適な低推力遷移軌道を設計するのは難しい.
凸最適化は,比較的短時間でロバストに最適解を得ることができ,また任意の局所最適解が大域的最適解になるという性質があるため,航空宇宙工学の分野でも注目されている.しかし,軌道最適化問題は非線形性が強いため,一般に凸最適化問題ではない.そこで,離散化と逐次的な線形化を行い繰り返し凸最適化問題を解くことで,非線形的な力学系における最適軌道を求めることができる.
この研究では,月周回有人拠点Gatewayへのミッションを見据えて,先行研究を拡張し,halo軌道からNRHO (Near-Rectilinear Halo Orbit)への最適遷移軌道をより広範に探索する手法を構築している.出発軌道と到着軌道上での位相(= 初期点と到着点の位置と速度)を含めた最適化問題に対し凸最適化を適用することで,低推力で燃料消費の小さい遷移軌道を設計する.
研究成果の一部はこちらの論文(J. Evol. Space Act.)から.
・中心多様体理論を用いた(準)周期軌道の設計(2019年4月ー2022年3月)
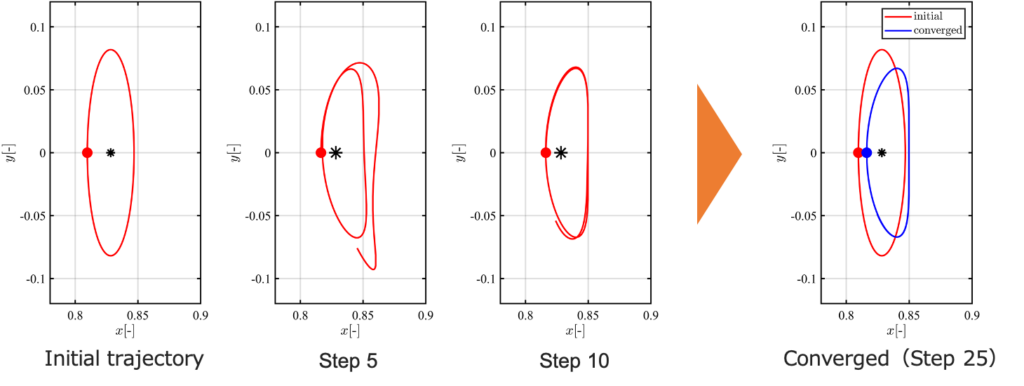
小惑星観測ミッションのための軌道設計では,小惑星近傍のとどまる軌道が重要となる.対象の天体まわりにとどまり続けることができれば,宇宙探査機は長い時間をかけて調査対象の天体の観測を行うことができる.このようなミッションのための軌道設計では,短時間で正確な軌道計算ができれば,多くの候補の中から最適なものを選択するということが可能となる.そのため,小惑星環境における効率の良い軌道設計手法が必要となる.
Center manifold methodは,逐次的に常微分方程式を解くことで,中心多様体上の軌道を計算する手法である.この手法の利点は,初期値を推定することなく,非線形な力学系の(準)周期軌道を計算でき,一様収束性があることである.Center manifold methodの利点は,初期値の推定やcontinuationを行うことなく,直接的に(準)周期軌道を求められることである.この研究では,center manifold methodを拡張し,小惑星観測ミッションに向けて(準)周期軌道を計算して解析できるようにする.
連星小惑星Didymosにおける計算例において,提案手法により小惑星の歪な質量分布を考慮してうまく中心多様体上の軌道を求めることができた.特に,リアプノフ軌道やハロー軌道のfamily,準周期軌道の計算を初期値を推定することなく行えることを示すことができた.
この研究の詳細については,こちらの論文(J. Guid. Control Dyn.)から.
Never give up work. Work gives you meaning and purpose and life is empty without it.
Stephen William Hawking
