・Trajectory Design and Optimization Based on Lobe Dynamics (Apr. 2022 – Current)
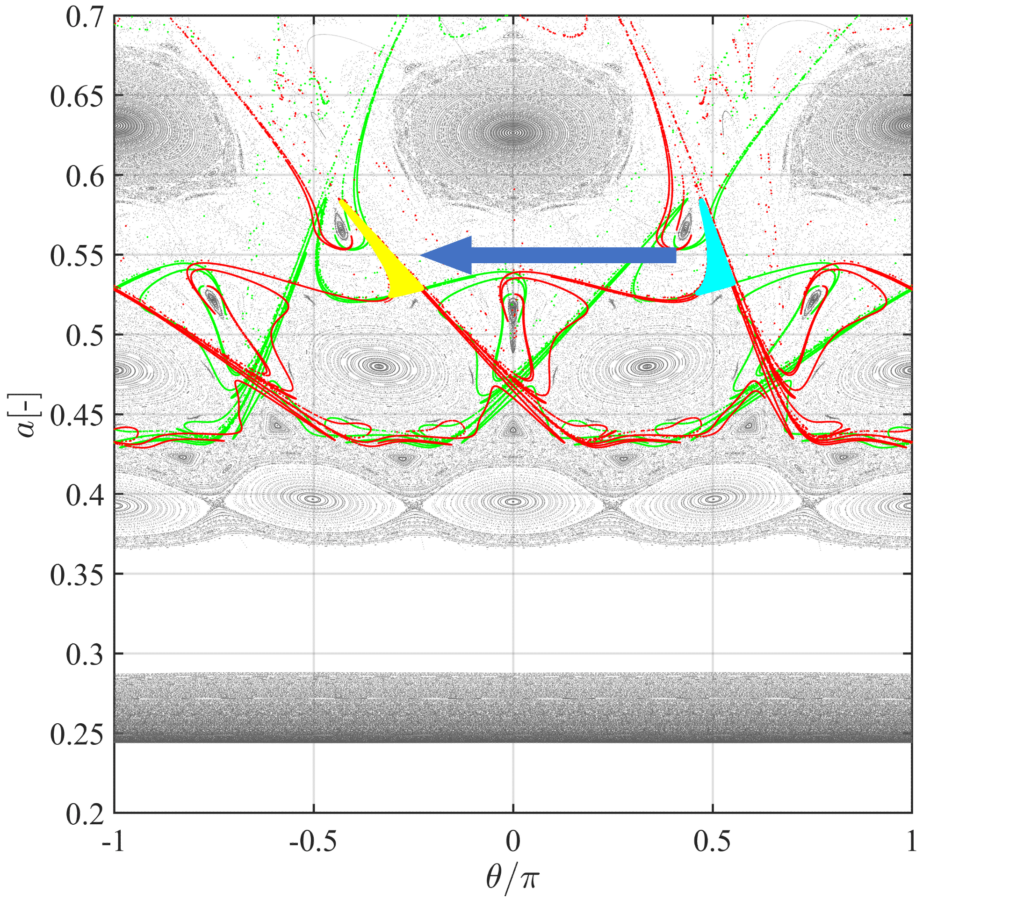
The dynamics of a spacecraft is known to be chaotic and highly nonlinear. These features make it difficult to optimize a trajectory in the computation. For lowering fuel consumption, invariant manifolds are among the essential dynamical structure of its natural dynamics.
One of the ways to leverage invariant manifolds is lobe dynamics. Lobe dynamics focuses on the “lobe,” the region determined by stable and unstable manifolds of a resonant orbit, and can reveal phase space transport of chaotic trajectories. Lobe dynamics has not been in the light because of its complex structures even though it enables involving chaotic motions in trajectory design. Thus, trajectory design based on lobe dynamics should be developed for fully exploiting natural dynamics and saving fuel consumption.
This study analyzes chaotic transfer trajectories based on lobe dynamics and proposes a new trajectory design methodology. We develop an algorithm to identify the lobes surrounded by stable and unstable manifolds of the resonant orbits in the periapsis Poincare map. Once a spacecraft is injected into one of the lobes, it transfers to the next lobe based on lobe dynamics describing the map of the lobes, i.e., a lobe sequence can be obtained. It is also demonstrated that the sequences of lobe dynamics of the resonant orbits are connected by appropriate impulsive thrust inputs.
・Low-Thrust Trajectory Design with Convex Optimization (Aug. 2021 – Current)
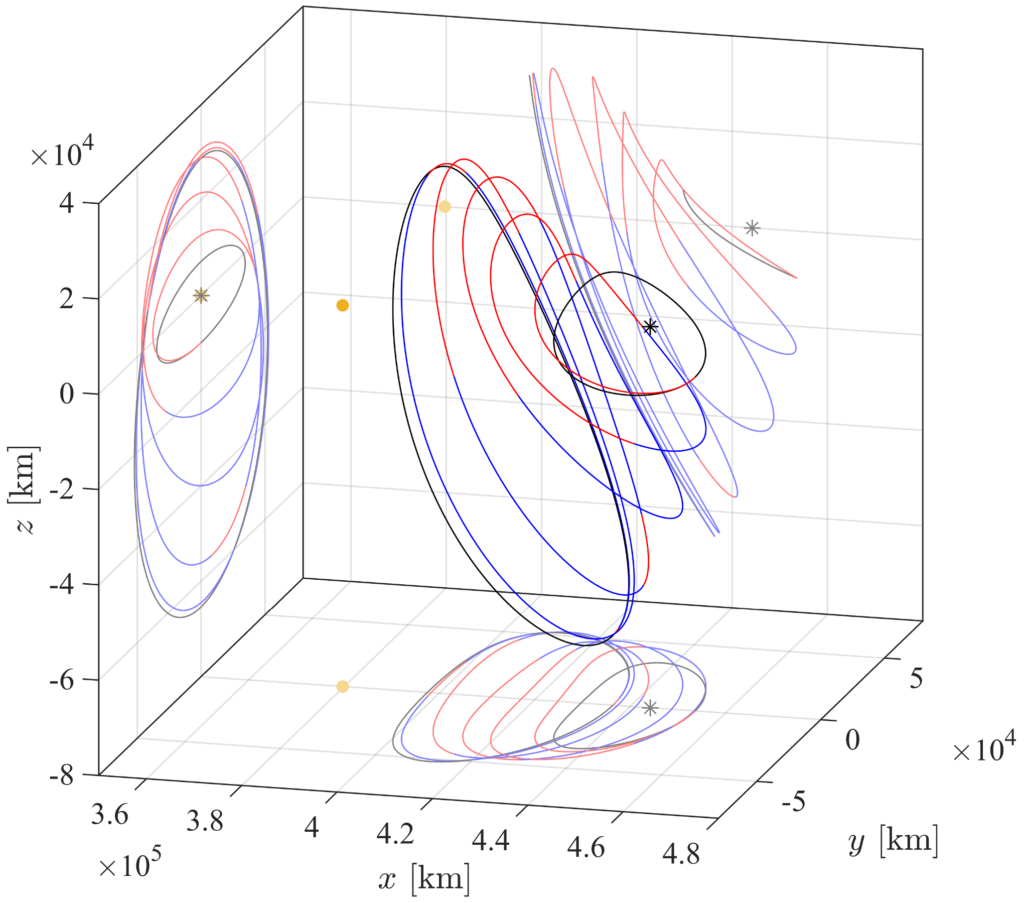
Recently, low-thrust propulsion, such as ion engines and solar sails, has been increasing attention because it has a high specific impulse and contributes to reducing fuel consumption. Although low-thrust trajectories enhance the efficiency of deep space missions, the optimal design of these trajectories is extremely difficult due to a high sensitivity with respect to initial conditions in the unstable orbital environment.
Convex optimization is a powerful tool for optimization in the field of aerospace engineering, including spacecraft trajectory design. The optimal solutions for convex optimization problems can be obtained in a robust manner by polynomial-time algorithms, and any local optimal solution satisfies the globally optimal condition. In general, trajectory optimization problems are nonconvex due to the nonlinear equations of motion. To deal with this nonlinearity, the optimization problem is convexified around the reference solution and iteratively solved so that its solution satisfies nonlinear constraints.
This study aims to extend the previous work and explore the optimal transfer to a near-rectilinear halo orbit (NRHO) more broadly for missions to the Gateway. The low-thrust minimum-fuel transfer from a halo orbit to an NRHO is designed by solving the convex optimization problem involving the departure and arrival phases as optimization parameters. Thus, this study constructs the framework to find the optimal phase-free orbit-to-orbit transfer.
Some of the results are available in our paper (Journal of Evolving Space Activities).
・Trajectory Design Based on Center Manifold Theory (Apr. 2019 – Mar. 2023)
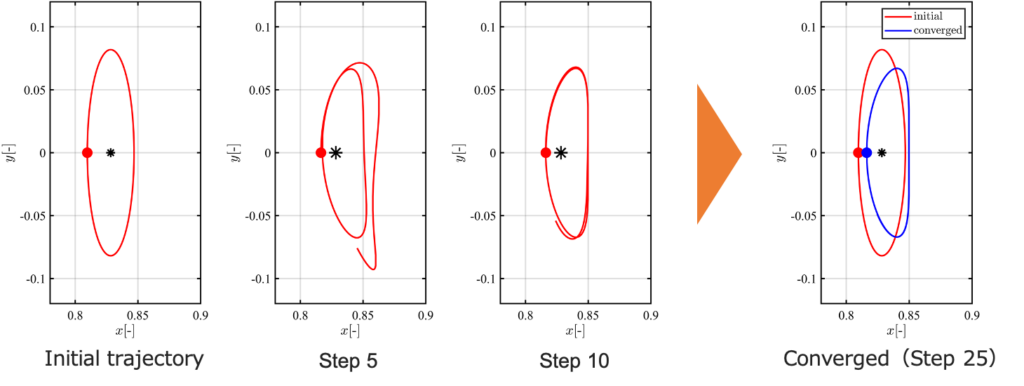
For the preliminary design of asteroid observation missions, the orbits bounded in the proximity of asteroids are particularly good candidates. When orbits are bounded to the asteroid/central body in concern, a spacecraft inserted in these orbits can observe the target for a long time. In the preliminary design, it is essential to find accurate solutions in a short time to pick up a suitable trajectory from several candidates. Thus, an efficient trajectory design method for the asteroid environment should be developed.
The center manifold method calculates trajectories on center manifolds by iteratively solving ordinary differential equations. This method is beneficial because it can deal with the full dynamics and has a uniform convergence property without an initial guess of a trajectory. This study extends the center manifold method to find the (quasi-) periodic orbits for asteroid observation missions.
The numerical examples under the dynamical environment of Didymos demonstrate that the center manifold method can successfully provide trajectories on center manifolds for a nonspherical mass distribution of asteroids. In particular, the calculation of Lyapunov and halo families and quasi-periodic orbits is executed without requiring a good initial guess.
Please check our paper (J. Guid. Control Dyn.) for more details.
Never give up work. Work gives you meaning and purpose and life is empty without it.
Stephen William Hawking
